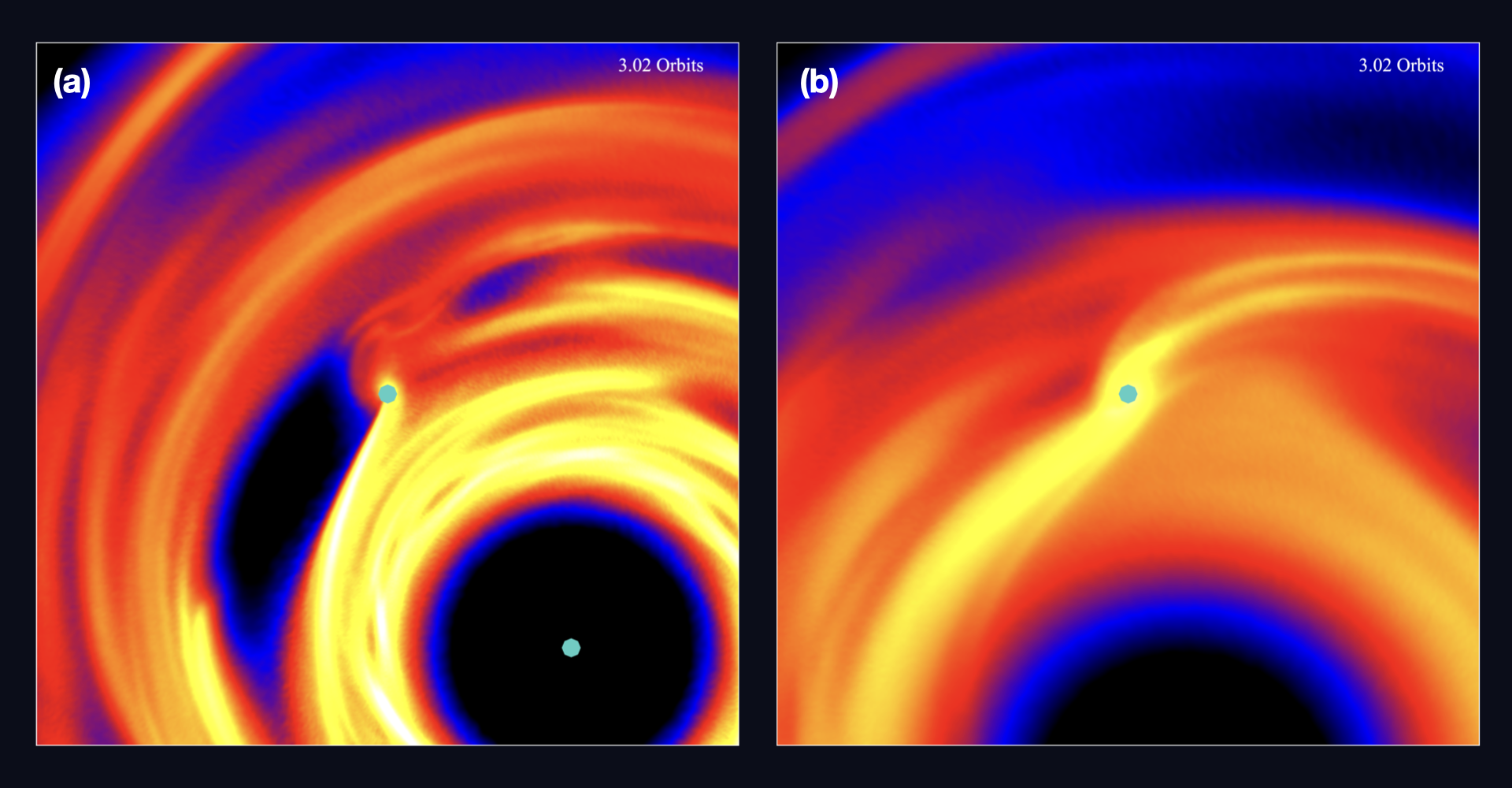
Analysis of coorbital material and torques
The coorbital material around the planet plays a key role in its migration. Initially the
planet begins its migration in the gravitationally unstable part of the disc, where the
density fluctuates a lot. These fluctuations results in an underdense region forming in
front of the planet which drives its inward migration in both models. Since the entire
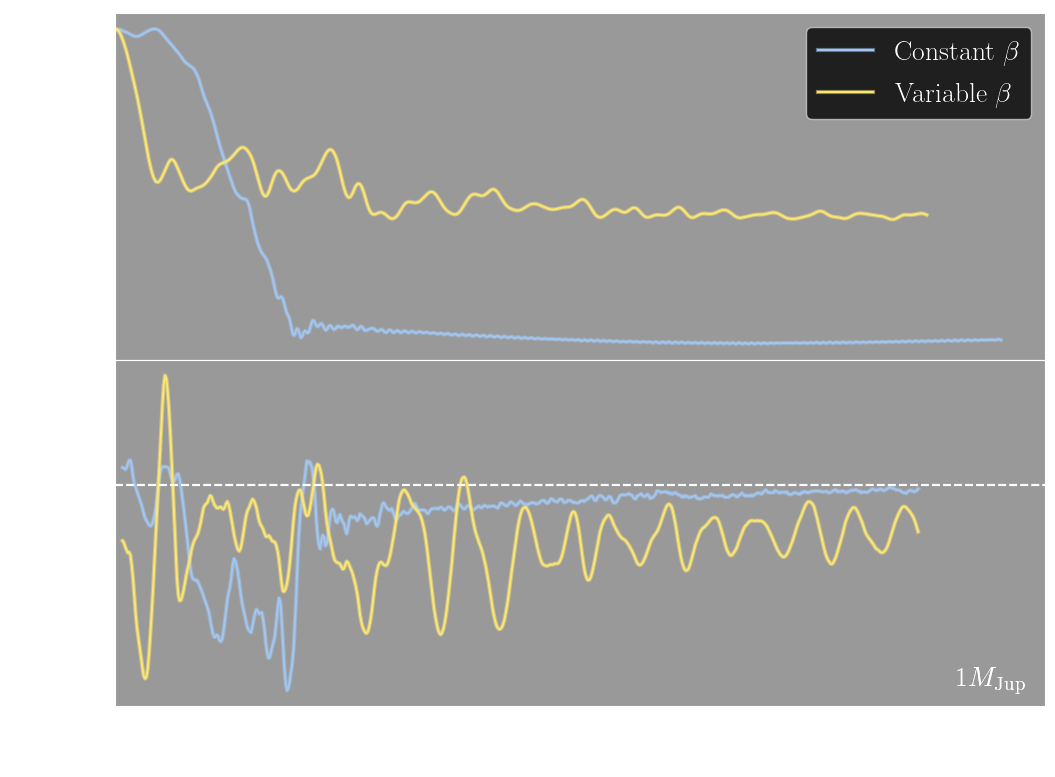
disc is gravitationally unstable with a constant \(\beta \), the corotation torque
remains negative throughout and the planet is unable to slow down (Figure 3a). However
with a variable \(\beta \), the planet is able to slow down once it reaches the
gravitationally stable inner disc. This smoother region results in the structure around
the planet becoming symmetric, thus decreasing the negative corotation torque and slows
the planet down (Figure 3b).
 blue text
blue text
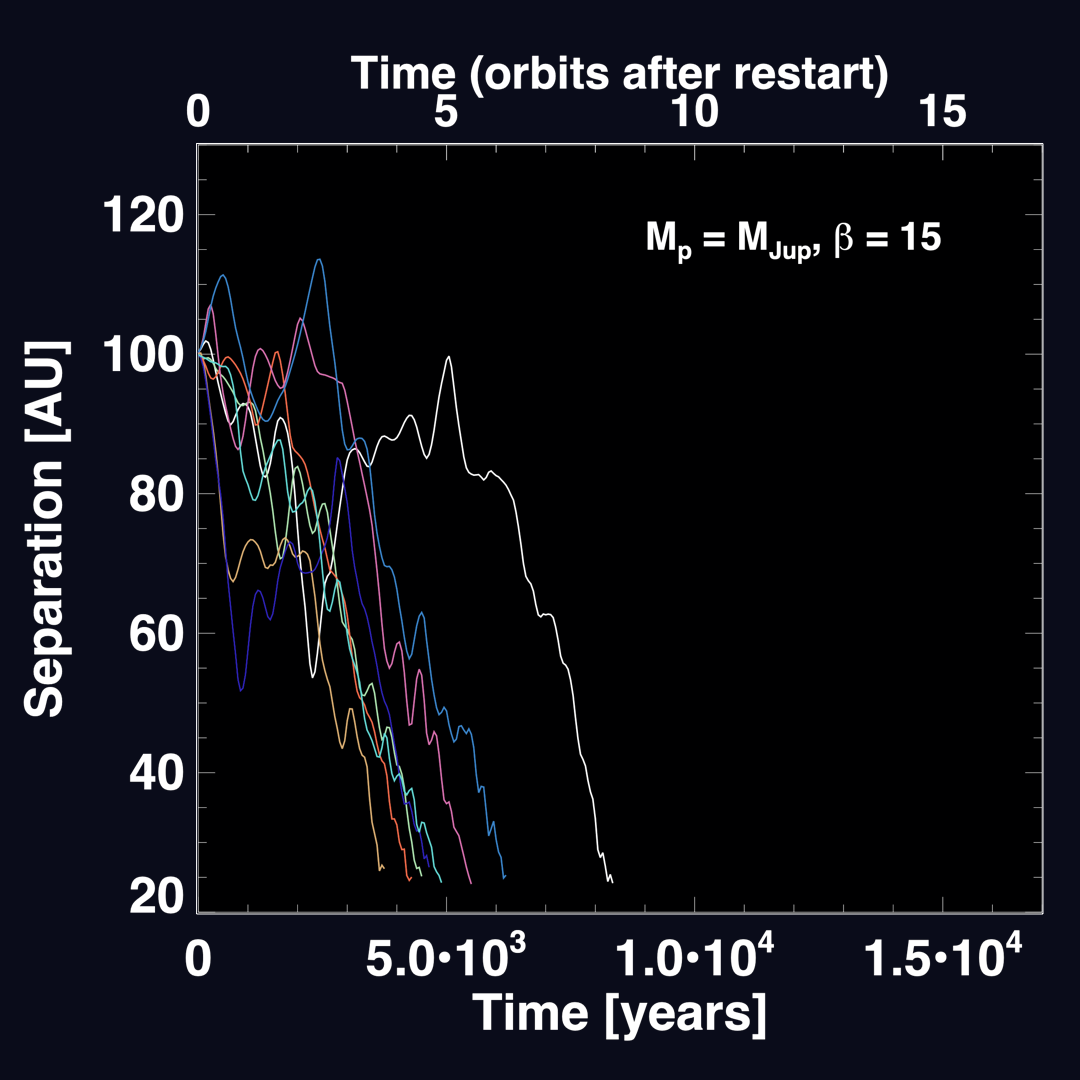 (Baruteau et al. 2011)
(Baruteau et al. 2011)