Hiding Gravitational Instability

Hiding Signatures of Gravitational Instability in Protoplanetary Discs

Sahl Rowther, Farzana Meru, Grant M. Kennedy, Rebecca Nealon, Christophe Pinte

Hover on blue text for more information.

Abstract

We carry out three dimensional SPH simulations to show that a migrating giant planet strongly suppresses the spiral structure in self-gravitating discs. We present mock ALMA continuum observations which show that in the absence of a planet, spiral arms due to gravitational instability are easily observed. Whereas in the presence of a giant planet, the spiral structures are suppressed by the migrating planet resulting in a largely axisymmetric disc with a ring and gap structure. Our modelling of the gas kinematics shows that the planet's presence could be inferred, for example, using optically thin ¹³C¹⁶O. Our results show that it is not necessary to limit the gas mass of discs by assuming high dust-to-gas mass ratios in order to explain a lack of spiral features that would otherwise be expected in high mass discs.

Motivation

When discs are young, they are expected to be quite massive. A characteristic feature of massive disc are large scale spiral features due to gravitational instabilities. However, observations of protoplanetary discs (Andrews et al. 2018 , Long et al. 2018) in the last few years have shown that most discs tend to be axisymmetric, with some also showing ring and gap structure. Even observations of very young Class 1 discs such as GY 91 (Sheehan & Eisner 2018) and IRS 63 (Segura-Cox et al. 2020) , both thought to be less than half a million years old, show rings & gaps.

Naturally, one might ask whether the lack of observed large scale spiral features in the midplane (even in very young discs) suggests that discs are not that massive? Assuming planets are the cause of the ring & gap structures observed, our aim is to investigate whether planet-disc interactions can hide signatures of gravitational instability.

Impact of planet on disc structure

The presence of the planet significantly impacts the structure. The planet suppresses the spiral structure and opens up a gap. Despite both discs retaining the same disc mass (~0.09M_⊙) within 200AU, the 2D Q plots show that the presence of the planet results in the disc becoming mostly gravitationally stable with Q > 1.7 throughout the disc. Without a planet, strong gravitationally unstable (Q < 1.7) arms are present (see Figure 1).

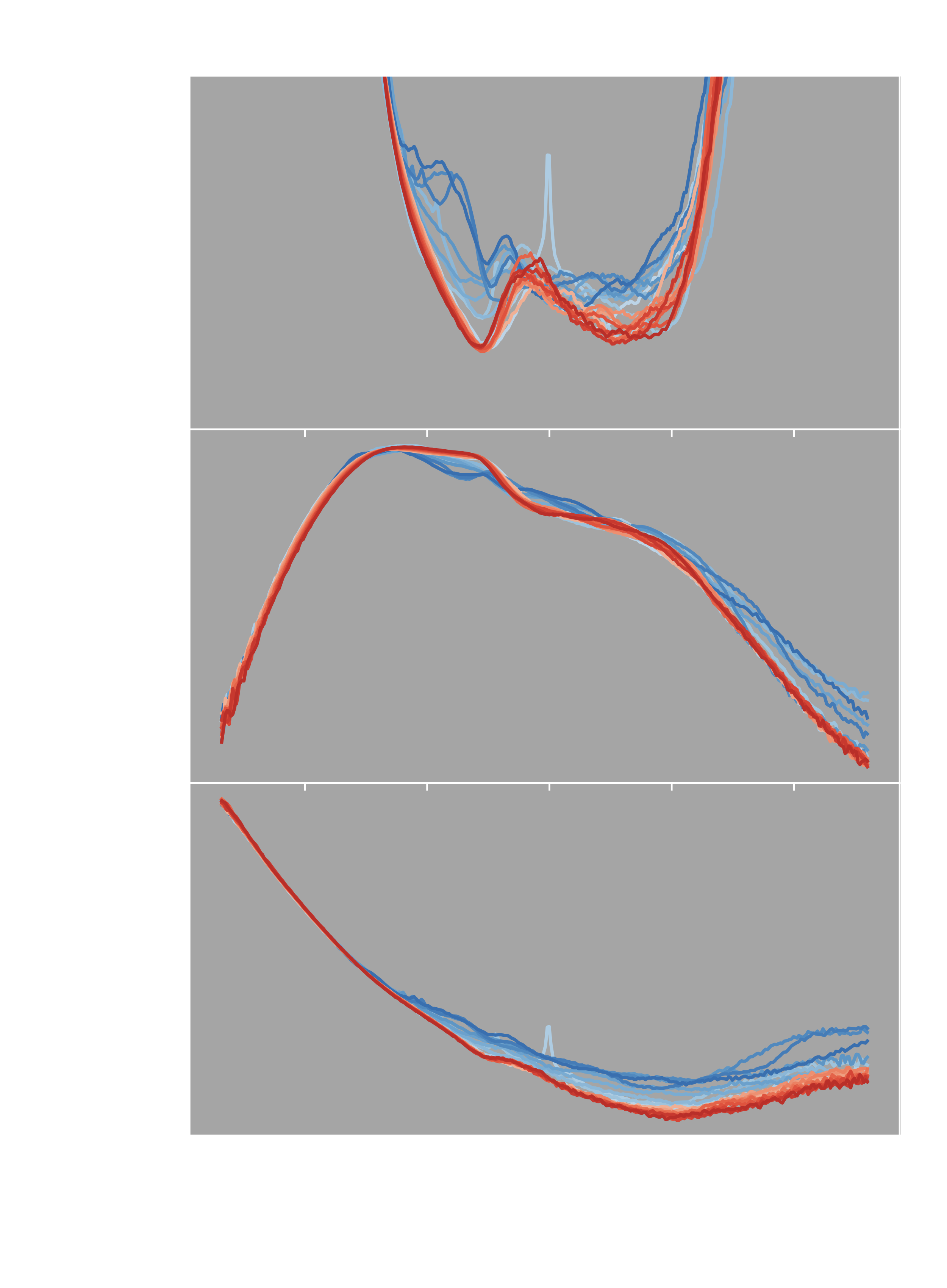
The dominant reason for the increase in Q is due to the planet's influence on the disc temperature, or equivalently the sound speed c_s, in the disc (see Figure 2). The spiral wakes generated by the planet as it migrates are regions of relative overdensities with respect to the disc background. The radially propagating spiral wakes can evolve into shocks. The exchange of momentum and energy between the density wakes and the disc at the shocks influence the global properties of the disc, heating it up.

**Figure 1:** Surface density (left) and 2D Toomre parameter Q (right) plots of a disc without a planet (top) and with a 3 Jupiter mass planet (bottom) at the end of the simulation. The 2D Toomre plots show how gravitationally unstable the disc is. The planet erases the spiral structure and is massive enough to carve out a gap. This results in a gravitationally stable axisymmetric disc.

**Figure 2:** Azimuthally averaged Toomre parameter, Q (top), surface density, Σ (middle), and the sound speed, c_s (bottom) for both the disc without a planet (red lines) and with a 3 Jupiter mass planet (blue lines) for the first 2 orbits after the planet is added. The darker shades represent later times. The increase in c_s due to the planet is the dominant reason for the increase in Q in the outer regions of the disc (beyond R ≈ 120AU), causing the disc to become gravitationally stable.

Mock ALMA continuum observations

To check if this was observable with ALMA, we created mock observations at 1.3mm. From the mock observations in Figure 3, it can be seen that without a planet, spiral arms due to gravitational instability would be readily apparent. Whereas with the planet, the only major non-axisymmetric feature that remains are the spiral arms caused by the planet.

Implications

This has important implications for observations. In some observations of axisymmetric discs, the observed dust mass can be high enough such that inferring the gas mass via a fixed dust-gas mass ratio results in a disc that is massive enough to be gravitationally unstable. But, a gravitationally unstable disc is expected to show spiral structure. Therefore in the absence of spiral structure, a higher dust-gas mass ratio is assumed when modelling the disc to ensure a less massive gravitationally stable disc. However this assumption is unnecessary as in the presence of a giant planet, we show that spiral structures expected from massive discs can be suppressed, thus appearing axisymmetric.

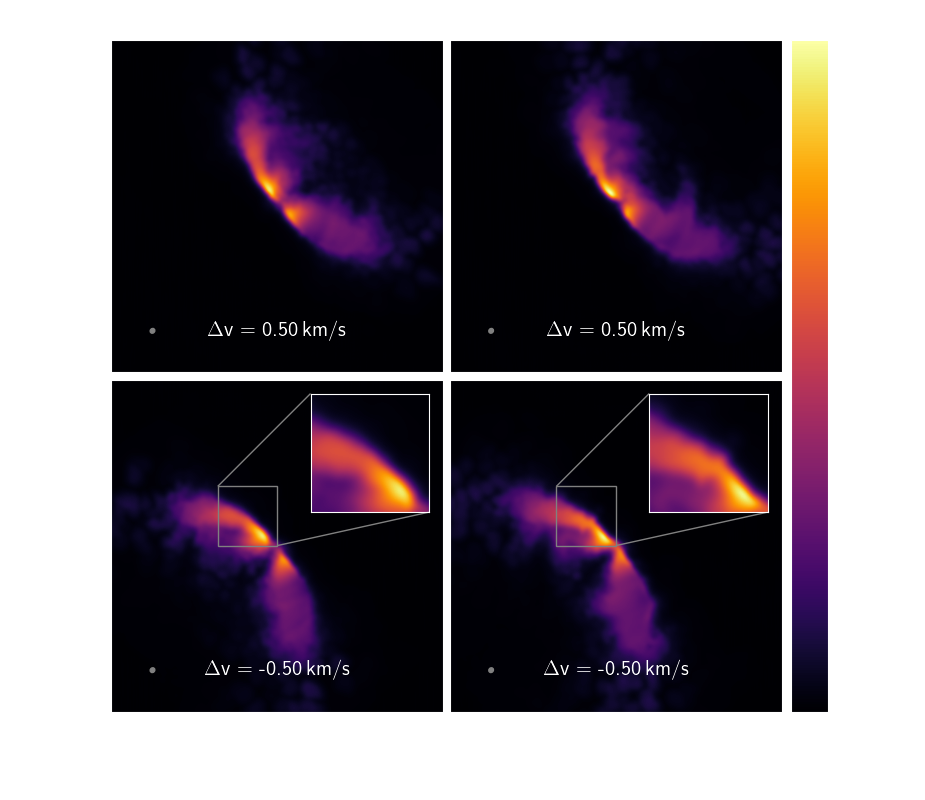
Figure 3: Mock observation (left) with integration times from 6-300 minutes, axisymmetric flux map (middle), and residual flux (right) of a disc without a planet (top) and with a 3 Jupiter mass planet (bottom). The presence of the planet results in a disc that no longer consists of spiral structure due to gravitational instability and appears to be more axisymmetric.

Presence of the planet in the disc kinematics

The gas kinematics can also be used to infer the presence of a planet. In general, the disc kinematics are dominated by Keplerian rotation. However if a disc is gravitationally unstable or a massive enough planet is present, there will be deviations from the Keplerian flow of the disc. In the case of a planet, the deviations from the Keplerian flow of the disc is localised near the planet’s location 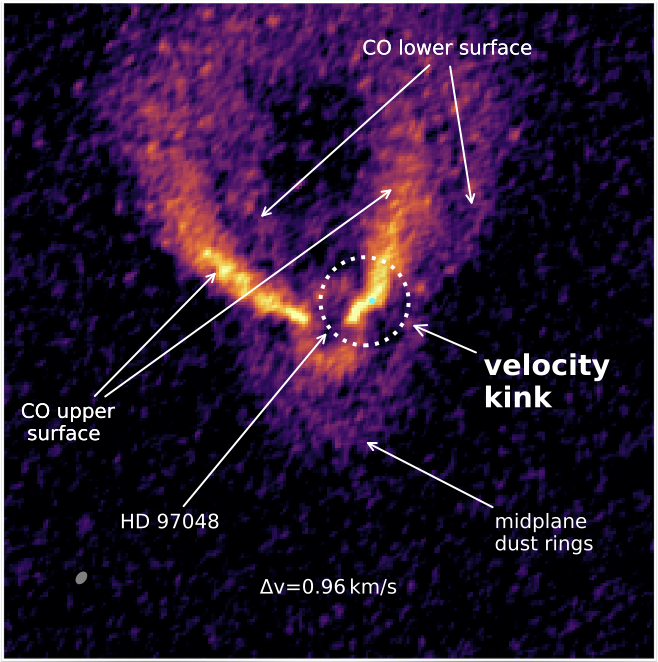(Pinte et al. 2019 ).

Figure 4 shows the synthetic ¹³C¹⁶O J=3-2 emission at velocity ±0.5 km/s from systemic velocity, both with and without the planet. A kink is visible in the optically thin ¹³C¹⁶O in the negative velocity channel within the vicinity of the planet, see bottom right inset. The bend in the emission profile in the bottom right inset is referred to as the kink. This is contrasted with the smooth velocity profile without a planet in the bottom left inset.

We can exclude large scale perturbations or any azimuthally symmetric mechanisms since the kink is not seen in the opposite velocity channel where the profile remains smooth.